Гармонические колебания Вселенной (Часть 8)
8. От ритмов атома к периодам видимого спектра
Цвета по приятности их гармоний
могут относиться между собою
подобно музыкальным созвучиям и
быть взаимно пропорциональными.
Аристотель, 384 – 322 гг до н. э.
8.1. Видимые и невидимые волны электромагнитных квантов
Меняю черное на белое.
Спросить: Серость
В. Борисов
Квант света, поглощаемый электоном при его выходе из атома водорода и излучаемый им при восстановлении своей позиции в атоме, относится к далёкой ультрафиолетовой области спектра, которая невидима для человека (см. 7.1, 7.2). Видимый диапазон электромагнитных колебаний расположен между инфракрасным излучением со стороны низких частот и ультрафиолетовым излучения со стороны высоких частот (см. рис. 7.1, 7.2, 7.4). Эти гармоники имеют частоту порядка 1015 Гц, поэтому для удобства написания их представляют в длинах волн. Нанометр (нм) это одна миллиардная часть метра (10-9 м).
8.2. Опыт И. Ньютона по разложению белого света в спектр радуги
Никто так не пополняет цвет
нации, как хамелеоны.
Л. Сухоруков
Представления о светомузыке, связанные с понятиями о мировой числовой гармонии, были заложены Пифагором (570—490 гг до н. э.) и его учениками. В основе физико-биологических теорий светового зрения лежит опыт Ньютона, проведенный спустя 2200 лет по расщеплению луча белого солнечного света на света радуги при его прохождении через призму [Википедия, Видимое излучение]. На рис. 8.1 часть пучка белого света отразилась от плоскости призмы без изменения, а преломленная часть луча разложилась в гармонический спектр от красного до фиолетового света.
Белый свет – это изобретение живых организмов, ведущих дневной образ жизни, которые мысленно складывают все видимые гармоники света от темно-красного до темно-фиолетового в один белый. Если изобразить цветной спектр полосками краски на средней части круга белой бумаги, а потом начать быстро вращать этот круг, то человек снова увидит чистый бесцветный белый круг, так как все цвета красок радуги снова сольются для наблюдателя в белую полосу, неотличимую от белого цвета центральной и внешней частей круга бумаги.
В спектрах разложения белого света призмой или атмосферными капельками воды в случае радуги (рис. 8.2) мы не наблюдаем такие известные нам света, как коричневый, розовый и пурпурный. Эти окраски являются результатом смешивания монохроматических (одноцветных) светов радуги. Глаз и мозг человека не могут определить, какие монохроматические гармоники света составляют эти смеси. Зрение в этих опытах сильно проигрывает слуху. Сочетания нот, формирующие аккорд, сравнительно легко распознаются любителями музыки и самими музыкантами.

Рис. 8.1. Взаимодействие луча белого света с призмой.
Фото: Spigget/commons.wikimedia.org
Кроме того, сложение некоторых светов, называемых дополнительными, формируют бесцветные серые пятна, соответствующие белому свету меньшей яркости. Дополнительные света и составы смешанных световых гармоник определяются экспериментальным путем. Например, пурпурный свет возникает при смешивании красного света с фиолетовым. Следует различать понятия света электромагнитных волн, формируемых Солнцем и земной атмосферой, от цвета художественной краски, который возникает в результате процессов поглощения и отражения. Здесь рассматриваются гармоники света, полученные только в результате оптического разложения солнечного излучения.

Радуга.
Фото: Vitalacharya/flickr.com
8.3. Октава И. Ньютона для цвето-музыки
Извините, мне трудно — я на
черном рояле не умею играть.
М. Задорнов
Ньютон расположил полученные им света радуги по кругу так, чтобы красный и фиолетовый концы спектра оказались рядом друг с другом (рис. 8.3). Этой световой радуге он противопоставил неравномерную музыкальную октаву из 7-ми нот (белые клавиши рояля). Таким образом Ньютон заложил физические основы световой музыки. Эту же музыкальную октаву из 7-ми нот через 160 лет применил соотечественник Ньютона Д. Ньюлендс при анализе химических элементов. Возможно, что это и было основной причиной, которая не позволила ему обнаружить подлинную периодичность химических элементов, в основе которой лежит октава из 8-ми нот.

Рис. 8.3. Круг светов Ньютона из книги «Оптика» (1704), показывающий взаимосвязь между семью светами и музыкальными нотами: Red – красный (D - ре), Orange - оранжевый (Е - ми), Yellow - желтый (F - фа), Green - зеленый (G - соль), Blue - голубой (A – ля), Indigo – синий (B - си), Violet – фиолетовый (C - до).
В отличие от 1) дискретных химических элементов с их десятью октавами из 8 нот (рис. 3.3), от 2) звуков рояля с 7-ю октавами из 12 нот (рис. 1. Увертюра), от 3) двадцати октав астрономических периодов из 16-ти (5.3) и 32 нот (6.1), в случае видимого спектра электромагнитных волн существует всего одна октава из плавно переходящих световых полос (рис. 8.1, 8.2), которой И. Ньютон противоставляет семь дискретных частот (рис. 8.3) из 12-ти нот звуковой октавы (3.1).
Процессы формирования светоощущений очень сложны. На рис. 8.4 показаны графики чувствительности глаз в видимом диапазоне. Существуют люди с повышенной чувствительностью восприятия во всем диапазоне или на отдельных участках видимого спектра. Графики чувствительности их глаз сильно отличаются от средних данных рис 8.4. Художники, как правило, различают в радуге гораздо большее количество цветов, чем принятое число 7.
Имеется и современное предложение по сопоставлению светов и музыкальной отктавы, которое отличается от предложения И. Ньютона (рис. 8.3). При использовании дополнительных смешанных соседних шести цветов набирается 12 цветов, соответствующих темперированному звукоряду из 12-ти нот: 1.Красный; 2.Оранжево-красный; 3.Оранжевый; 4.Оранжево-желтый; 5.Желтый; 6.Желто-зеленый; 7.Зелёный; 8.Сине-зелёный; 9.Синий; 10. Фиолетово-синий; 11.Фиолетовый; 12. Фиолетово-красный. Это и есть доступная обычному человеческому зрению «октава» цвета. [Википедия. Психология восприятия цвета]. Но такая световая октава соответствует только одной из семи звуковых октав рояля. Поэтому все света будут отражать звуки только одной звуковой октавы, что не соответствует конечной цели свето-музыки.
Зрение человека по числу светов и, особенно, октав всё же проигрывает слуху, но по количеству (90%) и важности получаемой человеком информации об окружающем нас мире электромагнитные колебания сильно опережают звуковые волны. Во многом это связано с тем, что свет может распространяться в вакууме и практически не затухает в сухом воздухе. Но информацию о строении Земли, о рыбных богатствах океана мы получаем только с помощью звуковых волн, для распространения которых нужна упругая среда.
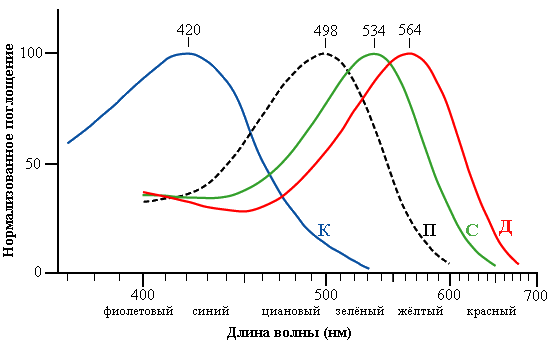
Рис. 8.4 Нормализованные графики чувствительности человеческих клеток-колбочек различных видов (К, С, Д) и клеток-палочек (П) к различным частям спектра. Ось длин волны дана в логарифмическом масштабе.
Иллюстрация: Maxim Razin/commons.wikimedia.org
Традиционно видимый спектр делится на 7 участков (диапазонов) светов (табл. 8.1), каждому из которых соответствуют свои границы длин электромагнитных волн в нанометрах (нм), или в терагерцах (ТГц) или в энергии фотонов (эВ) [Википедия. Электромагнитный спектр].
Таблица. 8.1. Частоты и энергии электромагнитных волн видимого спектра.
|
Цвет |
Диапазон длин волн, нм |
Диапазон частот, ТГц |
Диапазон энергии фотонов, эВ |
|
Фиолетовый |
380—440 |
790—680 |
2,82—3,26 |
|
Синий |
440—485 |
680—620 |
2,56—2,82 |
|
Голубой |
485—500 |
620—600 |
2,48—2,56 |
|
Зеленый |
500—565 |
600—530 |
2,19—2,48 |
|
Желтый |
565—590 |
530—510 |
2,10—2,19 |
|
Оранжевый |
590—625 |
510—480 |
1,98—2,10 |
|
Красный |
625—740 |
480—405 |
1,68—1,98 |
8.4. Взаимосвязи светов радуги и ритмов Вселенной
Проведите параллель
между женихами Пенелопы и
первой пунической войной.
Н. Тэффи
Ближнее инфракрасное излучение занимает диапазон от 405 ТГц (1,68 эВ) до 207 ТГц (0,857 эВ). Граница восприятия красного света зависит от индивидуальных особенностей каждого человека. Аналогичная ситуация наблюдается и на границе синего света. Поэтому к семи принятым можно добавить еще два света, назвав их тёмно-красным и тёмно-фиолетовым (см. рис. 8.1). При изображении такой световой октавы в виде круга, как это сделал И. Ньютон (рис. 8.3), она сомкнется своими границами с невидимыми частями спектра со стороны высоких и низких частот.
То есть эти света, тёмно-красный и тёмно-фиолетовый (табл. 8.2) можно считать подобными, как, например, ноты «до» соседних музыкальных октав. В результате 7 светов радуги преобразуются в полноценную гармоническую октаву из 8 нот и дополнительную ноту из следующей октавы, которая подобна первой из-за ее расположения на границе видимого спектра. Этой дополнительной «первой» нотой может быть темно-красный свет при начале отсчета от коротких длин волн, или темно-фиолетовый свет при начале отсчета от низких частот 480-405 ТГц, то есть от красного света (табл. 8.2).
Таблица 8.2. Линейные спектры (нанометры) для 8-ми нот из разных диапазонов видимого света.
Ноты |
Цвет |
Длины волн, нм |
Диапазоны длин волн, нм |
|
1 1 |
Темно фиолетовый |
380 |
380—410 |
|
2 8 |
Фиолетовый |
414 |
410—440 |
|
3 7 |
Синий |
452 |
440—485 |
|
4 6 |
Голубой |
493 |
485—500 |
|
5 5 |
Зелёный |
537 |
500—565 |
|
6 4 |
Жёлтый |
586 |
565—590 |
|
7 3 |
Оранжевый |
639 |
590—650 |
|
8 2 |
Красный |
697 |
650-700 |
|
1 1 |
Темно-красный |
760 |
700-760 |
Посмотрим, как эта гармоническая октава с повторением одной ноты 1 на границах видимого света радуги (табл. 8.2) соответствует геометрической прогрессии ритмов природы с нулевым периодом, равным обратному значению постоянной Ридбергера T0R = 3,041314*10-16 с. Вторая октава прогрессии Ридбергера (7.3) начинается с номера прогрессии R = 64 и содержит 32 ноты М (табл. 8.3). Октаве (TR8) с периодами из восьми нот (8.1) будет соответствовать каждая четвертая нота М, обозначенная в табл. 8.3 жирным шрифтом:
TR8 = T0R*2R /B = 3,041314*10-16*2 R /8 с (8.1)
где T0R – обратное значение константы Ридбергера (7.2), R - последовательность целых чисел и номера периодов прогрессии (7.3) и (8.1), B = 8 - количество природных гармоник в октаве (8.1). В табл. 8.3 они обозначены жирным шрифтом.
Оказалось, что значения длин волн световой радуги из табл. 8.2 сдвинуты относительно членов прогрессии Ридбергера TR (7.3) к центрам интервалов (табл. 8.3).
Таблица 8.3. Сопоставление октавы видимого спектра радуги (табл. 8.2) и октав (ТR и TR8) прогрессий Ридбергера (7.3 и 8.1)
|
Ноты, табл. 8.2 |
Ноты, М и М |
TR и TR8 |
LR, нм |
Длины волн, табл. 8.2 |
|
1 |
64 |
364,5069 |
||
|
2 |
65 |
372,4885 |
||
|
1 |
3 |
66 |
380,645 |
380 |
|
4 |
67 |
388,98 |
||
|
5 |
68 |
397,4976 |
||
|
6 |
69 |
406,2016 |
||
|
2 |
7 |
70 |
415,0963 |
414 |
|
8 |
71 |
424,1857 |
||
|
9 |
72 |
433,4742 |
||
|
10 |
73 |
442,966 |
||
|
3 |
11 |
74 |
452,6657 |
452 |
|
12 |
75 |
462,5778 |
||
|
13 |
76 |
472,7069 |
||
|
14 |
77 |
483,0579 |
||
|
4 |
15 |
78 |
493,6355 |
493 |
|
16 |
79 |
504,4447 |
||
|
17 |
80 |
515,4906 |
||
|
18 |
81 |
526,7783 |
||
|
5 |
19 |
82 |
538,3133 |
537 |
|
20 |
83 |
550,1008 |
||
|
21 |
84 |
562,1464 |
||
|
22 |
85 |
574,4558 |
||
|
6 |
23 |
86 |
587,0348 |
586 |
|
24 |
87 |
599,8892 |
||
|
25 |
88 |
613,025 |
||
|
26 |
89 |
626,4485 |
||
|
7 |
27 |
90 |
640,166 |
639 |
|
28 |
91 |
654,1838 |
||
|
29 |
92 |
668,5086 |
||
|
30 |
93 |
683,147 |
||
|
8 |
31 |
94 |
698,106 |
697 |
|
32 |
95 |
713,3925 |
||
|
1 |
96 |
729,0137 |
||
|
2 |
97 |
744,9771 |
||
|
1 |
3 |
98 |
761,2899 |
760 |
Таким образом было найдено соотношение средних значений видимых светов радуги и членов гармонических прогрессий с октавами из 32-х и 8-ми нот с начальным периодом, равным обратной величине физической константы Ридбергера (1.5) в Герцах.
Борис Берри. Специально для Великой Эпохи